常见算法和模板题
参照洛谷的算法标签
部分已有的上机考题目
张行功老师采用编程网格,选课同学能看到题目
校门外的树(暴力模拟)
NOIP 2005 普及组
算法:暴力模拟
l,m = map(int,input().split())
removed = [False]*(l+1)
for _ in range(m):
a,b = map(int,input().split())
for i in range(a,b+1):
removed[i] = True
print(removed.count(False))-
时间复杂度: 。最坏情况下,如果这 个区间都很长,你需要遍历很多次整个数组。
-
空间复杂度: 。需要一个长度为 的数组。
算法:区间合并+一点点贪心
l, m = map(int, input().split())
ans = l + 1
removed = []
for _ in range(m):
u, v = map(int, input().split())
removed.append((u, v))
removed.sort()
merged = []
for interval in removed:
if not merged or merged[-1][1] < interval[0]:
merged.append(interval)
else:
merged[-1] = (merged[-1][0], max(merged[-1][1], interval[1]))
print(ans - sum(v - u + 1 for u, v in merged))-
时间复杂度: 。主要消耗在排序上,之后的遍历合并是线性的 。注意:这个复杂度与马路的长度 无关!
-
空间复杂度: 。只需要存储 个区间。
括号匹配(复杂模拟)
算法标签:复杂模拟、字符串、栈
n = int(input())
pairs = {')':'(', ']':'[', '}':'{'}
for _ in range(n):
s = input().strip()
stack = []
valid = True
for char in s:
if char in '([{':
stack.append(char)
else:
if not stack or stack[-1] != pairs[char]:
valid = False
break
stack.pop()
if valid and not stack:
print("YES")
else:
print("NO")旅行家的预算(贪心)
算法标签:复杂贪心
两种可供参考的思路:
- 每到一个加油站,考虑刚刚好加足够跑到下一个比当前加油站油价更便宜的加油站的油,如果没有更便宜的加油站了,则加满油箱。这里贪心的点在于:每次我们只考虑我们能看到的一箱油最大可行驶距离这么大的区域,如果能找到更便宜的油,就只加足够的油到达那里,否则就优先使用最便宜的油,直接加满。
prices = []
S, C, L, P0, N = map(float, input().split())
prices.append((0.0, P0))
for _ in range(int(N)): # 注意类型转换
D, P = map(float, input().split())
prices.append((D, P))
prices.append((S, 0.0)) # 终点,价格设为0方便处理
prices.sort()
# 贪心思想:每次加刚刚好足够到达下一个比当前加油站便宜的加油站的油量,如果满箱油可达范围内找不到更便宜的就直接加满
total_cost = 0.0
current_fuel = 0.0
max_distance = C * L
for i in range(len(prices) - 1):
distance_to_next = prices[i + 1][0] - prices[i][0]
if distance_to_next > max_distance:
print("No Solution")
break
# 查找下一个比当前加油站便宜的加油站
next_cheaper_index = -1
for j in range(i + 1, len(prices)):
if prices[j][1] < prices[i][1]:
next_cheaper_index = j
break
# 没有更便宜的加油站或者更便宜的加油站不可达,直接加满油
# 计算到下一个更便宜加油站所需的油量
distance_to_cheaper = min(prices[next_cheaper_index][0] - prices[i][0], max_distance) # 这里利用了next_cheaper_index 初值是-1的特性,直接取min
needed_fuel = (distance_to_cheaper / L) - current_fuel
if needed_fuel > 0:
total_cost += needed_fuel * prices[i][1]
current_fuel += needed_fuel
# 消耗到下一个加油站的油量
current_fuel -= distance_to_next / L
else:
print(f"{total_cost:.2f}")- 到每一个加油站都加满油,如果比之前的油便宜,可以“退掉”之前加的油,在汽车行驶时优先使用最便宜的油(因为在贪心思想下要让成本最低,到终点站时必然是一滴油也不会剩下的,都在路上烧掉了。我们为了能够“退掉”更贵的油,要优先烧掉便宜的)
prices = []
S, C, L, P0, N = map(float, input().split())
prices.append((0.0, P0))
for _ in range(int(N)): # 注意类型转换
D, P = map(float, input().split())
prices.append((D, P))
prices.append((S, 0.0)) # 终点,价格设为0方便处理
prices.sort()
# 贪心思想:,默认加满油箱,然后到下一个加油站,如果价格比之前的低,则把之前剩下的油“倒掉”,换成新的油(贪心)加满 依次类推
# 需要有一个元组列表记录当前油箱的情况,开车时优先烧最便宜的油
# 如果出现了无法到达的情况,则输出 No Solution
total_cost = prices[0][1] * C # 出发时加满油箱
current_fuel = [(prices[0][1], C)] # (价格,油的数量)
for i in range(1, len(prices)):
distance = prices[i][0] - prices[i - 1][0]
# 如果满箱油也到达不了下一个加油站
if distance > C*L:
print("No Solution")
break
# 消耗当前油箱的油
current_fuel.sort() # 按价格从低到高使用油
fuel_needed = distance / L
while fuel_needed > 0 and current_fuel:
price, amount = current_fuel[0]
if amount > fuel_needed:
current_fuel[0] = (price, amount - fuel_needed)
fuel_needed = 0
else:
fuel_needed -= amount
current_fuel.pop(0)
# 到达加油站
new_price = prices[i][1]
# 与当前油箱中所有种类的油分别比较价格,从高到低决定是否退掉
while current_fuel and current_fuel[-1][0] > new_price:
price, amount = current_fuel.pop()
total_cost -= price * amount # 把旧油的钱退掉
# 无论如何都要加满油箱
fuel_needed = C - sum(amount for _, amount in current_fuel)
current_fuel.append((new_price, fuel_needed))
total_cost += new_price * fuel_needed
else:
print(f"{total_cost:.2f}")八皇后(DFS)
深度优先搜索模板题目
深搜其实也是一种递归算法(自己调用自己),而递归(函数调用)和迭代(条件循环)通常情况下可以互相转换,故这里不再单独列出递归相关的算法题目。在使用递归时,有一些常见的技巧:
- 提高递归深度上限:
import sys
sys.setrecursionlimit(20000) # 根据需要调整数值- 自动记忆化(lru_cache装饰器):
from functools import lru_cache
@lru_cache(maxsize=None)
def dfs(state):
pass使用lru_cache有一些要求,包括函数参数必须可哈希、函数必须是纯函数(如果修改外部状态就不能用lru_cache)等
这道八皇后问题的输出格式,明显提醒我们应该采用深度优先搜索(只需要输出前三个完整解,不关注搜索的广度),示例代码如下:
# 深度优先搜索模板
n = int(input())
cols = [0] * (n + 1) # cols[i]表示第i行的皇后放在第cols[i]列
count = 0
results = []
def is_valid(row, col):
for prev_row in range(1, row):
# 按行搜索保证了不在同一行
# 我们需要验证不在同一列和不在同一对角线
if cols[prev_row] == col or abs(cols[prev_row] - col) == abs(prev_row - row):
return False
return True
def dfs(row):
# 我们在前面的课程中提到过不要把列表作为函数的参数,这里采用全局变量就是一种不错的解决方案
global count
if row > n:
count += 1
if count <= 3:
print(' '.join(map(str, cols[1:])))
return
# 搜索下一行的所有位置
for col in range(1, n + 1):
if is_valid(row, col):
cols[row] = col
# 深度优先,继续搜索下一行
dfs(row + 1)
cols[row] = 0 # 回到初始状态
dfs(1)
print(count)如果使用洛谷平台提交,就会收获两个TLE的测试点。
解决方案:
-
打表: 输入数据就是一个整数且范围较小,可以把
n = 11/12/13这几个算得慢的结果直接写死在代码里(先在自己电脑上跑一遍得到答案),提交时根据输入判断,直接输出结果即可。 -
优化判断合法情况的逻辑: 注意到主对角线(从左上到右下)的坐标都满足
row - col相等,副对角线(从右上到左下)的坐标都满足row + col相等,因此我们可以使用三个布尔数组分别记录哪些列、主对角线、副对角线已经被占用,从而将合法性判断的时间复杂度从降低到。
# 深度优先搜索模板
n = int(input())
cols = [0] * (n + 1) # cols[i]表示第i行的皇后放在第cols[i]列
count = 0
results = []
# 标记数组:
# vis[j] 表示第 j 列是否被占用
# to_left[x+i] 表示坐标 (x,i) 所在的 "+" 型(或主)对角线是否被占用
# to_right[x-i+n] 表示坐标 (x,i) 所在的 "-" 型(或副)对角线是否被占用
vis = [False] * (n + 1)
to_left = [False] * (2 * n + 1)
to_right = [False] * (2 * n + 1)
def dfs(row):
# 我们在前面的课程中提到过不要把列表作为函数的参数,这里采用全局变量就是一种不错的解决方案
global count
if row > n:
count += 1
if count <= 3:
print(' '.join(map(str, cols[1:])))
return
# 搜索下一行的所有位置
for col in range(1, n + 1):
# 常数时间判断:只需检查列和两个对角线的标记
if not vis[col] and not to_left[row + col] and not to_right[row - col + n]:
# 标记并放置皇后
cols[row] = col
vis[col] = True
to_left[row + col] = True
to_right[row - col + n] = True
# 深度优先,继续搜索下一行
dfs(row + 1)
# 回溯,取消标记
vis[col] = False
to_left[row + col] = False
to_right[row - col + n] = False
cols[row] = 0 # 回到初始状态
dfs(1)
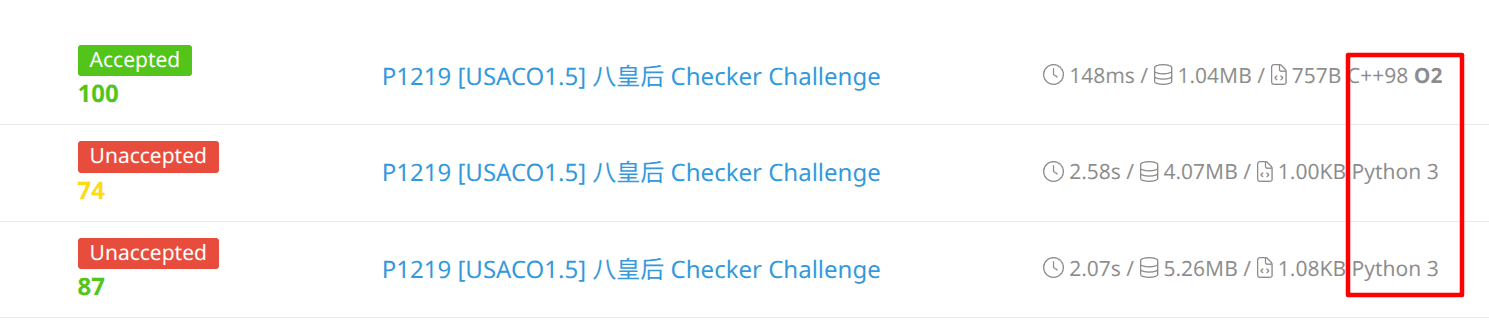
print(count)此时再提交,得到结果:还有一个点仍然TLE,事实上这种方案在C/C++下应该是可以通过的,但Python的执行效率较低,仍然无法通过最后一个测试点。
- 位运算优化: 基本思想:用二进制位从右到左表示实际第1列到第n列的占用情况,利用位运算的左移右移、按位与按位或等操作来替代数组访问,从而进一步提高效率。
# 深度优先搜索模板
n = int(input())
cols = [0] * (n + 1) # cols[i]表示第i行的皇后放在第cols[i]列(1-based)
count = 0
def dfs(k, r, z, f):
# k: 当前行(1-based)
# r: 已占用的列,二进制表示,从低到高表示第1列到第n列,为0表示未占用,为1表示已占用
# z: 主对角线占用,同理,二进制表示当前已经被占了的主对角线
# f: 副对角线占用,同理
global count
if k > n:
count += 1
if count <= 3:
print(' '.join(map(str, cols[1:])))
return
# 合并,目前所有被占据位置的二进制表示
s = r | z | f
# 按列 1..n 依次检查
for i in range(1, n + 1):
# 第1列对应二进制的第0位(最右边的一位),第2列对应二进制的第1位,以此类推
# 检查第i列是否被占用
if not (s & 1):
bit = 1 << (i - 1) # 表示即将在第i列放置皇后
cols[k] = i # 更新当前行皇后的位置
"""
!!! 重要
主对角线:向下一行搜索时,被占用的主对角线位置需要左移一位,(对应于棋盘上向右下角移动一位)
副对角线:向下一行搜索时,被占用的副对角线位置需要右移一位,(对应于棋盘上向左下角移动一位)
这样才能正确表示下一行的对角线占用情况
"""
dfs(k + 1, r | bit, (z | bit) << 1, (f | bit) >> 1)
cols[k] = 0 # 恢复到未放置状态
# 检查下一列(二进制移动到下一位)
s >>= 1
dfs(1, 0, 0, 0)
print(count)然而还是会超时,甚至比刚刚的方法还慢了,看来Python对位运算的优化做的不是很好。而换用C++后最大的数据点也能够控制在100ms,成功通过此题。
迷宫寻路(BFS)
DFS/BFS 模板题目
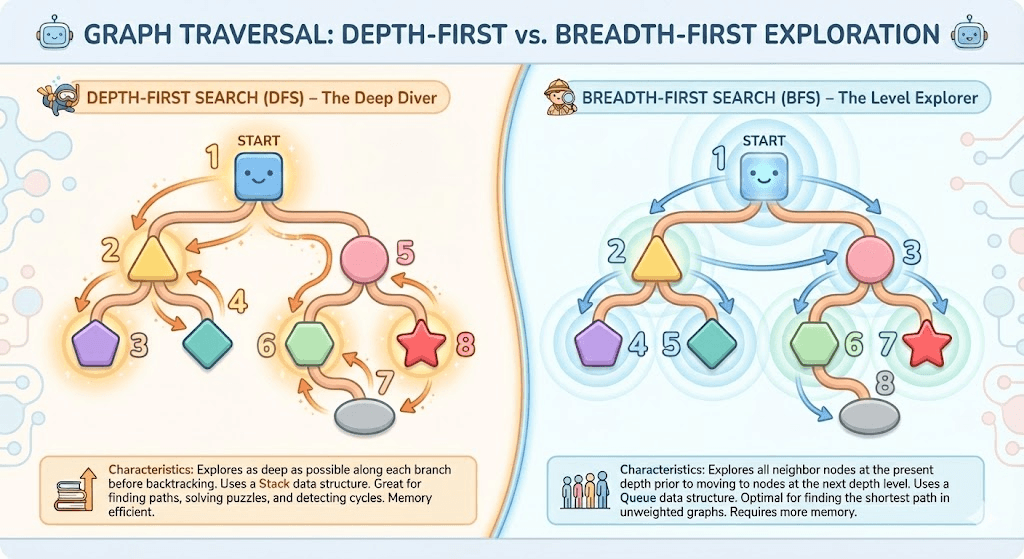
深度优先搜索和宽度优先搜索之间的关系:
- DFS 使用栈(递归调用栈或显式栈)实现,适合用于需要探索所有可能路径的场景,如组合问题、排列问题等。
- BFS 使用队列实现,适合用于寻找最短路径或最少步骤的问题,如迷宫问题、图的最短路径等。
这道题询问的是“能否达到”,显然搜到一种方案就可以停止,但如果一直走不到就要遍历所有可能的路径,实际上DFS和BFS都可以使用。而如果问你最短路径,那BFS就是最优的选择,因为按照广度进行遍历,深度是依次推进的,如果5步能够解决问题,BFS在第5步就会停止,DFS则会继续深入下去,直到所有情况都遍历完再结算最短路径,显然复杂度高了不少
下面让Nano Banana生成了一个展示二者区别的图片:
深度优先搜索:
# 解除递归深度限制
import sys
sys.setrecursionlimit(100000)
n, m = map(int, input().split())
maze = [input().strip() for _ in range(n)]
# DFS
visited = [[False] * m for _ in range(n)]
directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
flag = False
def is_valid(x, y):
# 这里实际上利用了 Python 的短路特性,先判断边界,再判断迷宫内容和访问状态 实际并不会产生越界错误
return 0 <= x < n and 0 <= y < m and maze[x][y] == '.' and not visited[x][y]
def dfs(x, y):
global flag
if flag or (x == n - 1 and y == m - 1):
flag = True
return
visited[x][y] = True
for dx, dy in directions:
nx, ny = x + dx, y + dy
if is_valid(nx, ny):
dfs(nx, ny)
dfs(0, 0)
print("Yes" if flag else "No")广度优先搜索:
n, m = map(int, input().split())
maze = [input().strip() for _ in range(n)]
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
def is_valid(x, y):
return 0 <= x < n and 0 <= y < m and maze[x][y] == '.'
# BFS 列表实现
def bfs():
visited = [[False] * m for _ in range(n)]
queue = [(0, 0)]
visited[0][0] = True
while queue:
x, y = queue.pop(0)
if (x, y) == (n - 1, m - 1):
return "Yes"
for dx, dy in directions:
nx, ny = x + dx, y + dy
if is_valid(nx, ny) and not visited[nx][ny]:
visited[nx][ny] = True
queue.append((nx, ny))
return "No"
print(bfs())也可以使用python内置的collections.deque来实现队列,从而提高效率:
# ... Stay the same up to is_valid function ...
# BFS python内置deque实现
from collections import deque
def bfs():
queue = deque()
queue.append((0, 0))
visited = [[False] * m for _ in range(n)]
visited[0][0] = True
while queue:
x, y = queue.popleft()
if (x, y) == (n - 1, m - 1):
return "Yes"
for dx, dy in directions:
nx, ny = x + dx, y + dy
if is_valid(nx, ny) and not visited[nx][ny]:
visited[nx][ny] = True
queue.append((nx, ny))
return "No"
print(bfs())